الوحدة التي يمكننا استخدامها لقياس فرق الجهد عبر أي نقطة تسمى أ فولت . الفولت هو فرق الجهد المطبق عبر المقاومة البالغة 1 أوم، وسوف يؤدي إلى تدفق التيار الكهربائي من الطرف الأعلى إلى الطرف السفلي.
تتدفق الاختلافات المحتملة دائمًا من القيمة المحتملة الأعلى إلى القيمة المحتملة الأقل. يمكننا أيضًا تعريف 1V على أنه الجهد عندما يتم ضرب 1 أمبير من التيار بمقاومة 1 أوم. لوصف الفرق المحتمل، يتم استخدام صيغة قانون أوم، والتي تساوي الخامس = التاسعR .
وفقا لقانون أوم، يزداد التيار في الدوائر الخطية مع زيادة فرق الجهد. إن الدائرة التي لها فرق جهد كبير بين أي نقطتين ستؤدي إلى تدفق تيار أكثر عبر هاتين النقطتين في الدائرة.
على سبيل المثال، لنفترض مقاومة بقيمة 10 أوم، والجهد المطبق عبر أحد طرفيها هو 8V. وبالمثل، فإن الجهد عبر الطرف الآخر هو 5V. لذلك سوف نحصل على فرق جهد 3V (8V-5V) على طرف المقاومة. للعثور على التيار عبر المقاومة، يمكننا استخدام قانون أوم. سيكون تيار هذه الدائرة 0.3A.
فإذا قمنا بزيادة الجهد من 8 فولت إلى 40 فولت فإن فرق جهد المقاومة سيصبح 40 فولت – 5 فولت = 35 فولت. سيؤدي هذا إلى 3.5A من التدفق الحالي. عندما يزداد فرق الجهد عبر المقاومة، سيؤدي ذلك أيضًا إلى زيادة التيار.
لقياس جهد أي نقطة داخل الدائرة، علينا مقارنتها بالنقطة المرجعية المشتركة. نستخدم عادةً 0V أو الدبوس الأرضي كنقطة مرجعية في الدائرة لقياس فرق الجهد.
مخطط سريع
ما هو الفرق المحتمل
فرق الجهد، المعروف أيضًا باسم الجهد، هو مفهوم أساسي في الكهرباء. وهو يصف بشكل أساسي الفرق في طاقة الوضع الكهربائية بين نقطتين داخل الدائرة الكهربائية. يؤدي اختلاف الجهد بين نقطتين إلى انتقال الشحنة من نقطة جهد أعلى إلى نقطة جهد أقل. سيؤدي ذلك إلى تدفق التيار الكهربائي. نحن نقيس فرق الجهد بالفولت (V)، وهو عامل حاسم في تحديد كيفية سلوك الكهرباء في الدائرة وكيفية عمل الأجهزة الكهربائية.
مثال الفرق المحتمل
في الصورة، الجهد المطبق عبر المقاومة عند أحد طرفيها هو 10 فولت. الجهد على الطرف الثاني للمقاومة هو 5 فولت.
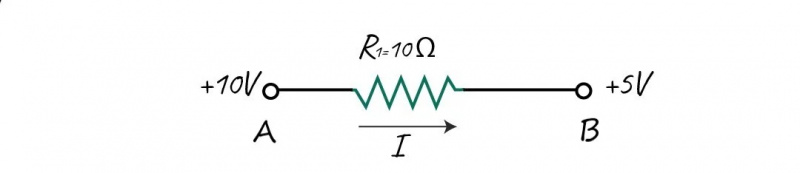
لحساب فرق الجهد عبر نهاية المقاومة، اطرح الجهد الأعلى من الجهد الأدنى:
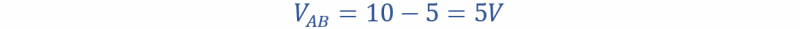
فرق الجهد المحسوب عبر المقاومة هو 5V.
التيار في المقاوم يتناسب مع الإمكانات المطبقة. إذا كان فرق الجهد بين أي نقطتين أكبر، فسوف ترى تدفق تيار كبير.
استخدم قانون أوم للعثور على التيار.

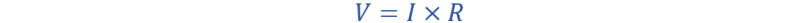
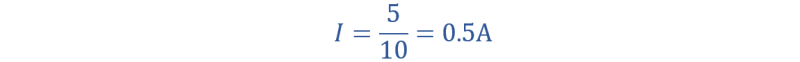
الآن، قم بزيادة الجهد من 10 فولت إلى 20 فولت عبر أحد طرفي المقاومة ومن 5 فولت إلى 10 فولت عبر الطرف الآخر. سيصبح فرق الجهد 10 فولت. وباستخدام قانون أوم يمكنك إيجاد التيار المار عبر المقاومة التي تبلغ 8 أمبير.
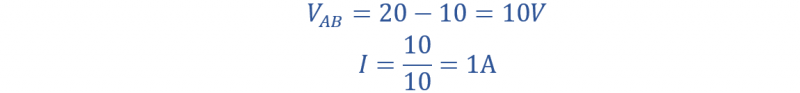
الشحنة الكهربائية تؤدي إلى تدفق التيار الكهربائي. لكن الإمكانات لا تتحرك أو تتدفق جسديًا. يتم تطبيق الإمكانات عبر أي نقطتين محددتين في الدائرة.
لإيجاد الجهد الإجمالي للدائرة، علينا جمع جميع الجهود المتصلة في الدائرة المتوالية. هذا يعني أنه عندما يكون لديك مقاومات (في 1 ، في 2 ، و في 3 ) متصلة على التوالي، يمكنك ببساطة جمع الفولتية للعثور على الجهد الإجمالي:
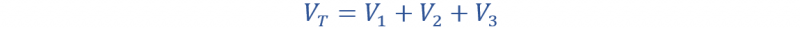
من ناحية أخرى، عند توصيل المقاومات على التوازي، يظل الجهد عبر كل مقاومة أو عنصر كما هو. على التوازي، يكون الجهد عبر كل مقاومة متساويًا، ويمكن التعبير عنه على النحو التالي:
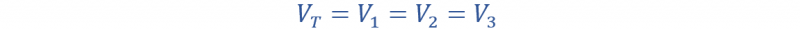
شبكة مقسم الجهد
نحن نعلم أنه إذا قمنا بتوصيل مقاومات متعددة على التوالي عبر فرق جهد، فستكون مقاومة جديدة دائرة مقسم الجهد سيشكل. تقوم هذه الدائرة بتقسيم جهد الإمداد بين المقاومات بنسبة محددة. يحصل كل مقاوم على جزء من الجهد نسبة إلى مقاومته.
ينطبق مبدأ دائرة مقسم الجهد هذا فقط على المقاومات المتصلة على التوالي. إذا قمنا بتوصيل المقاومات على التوازي، فسينتج عن ذلك إعداد مختلف تمامًا، وهو ما يسمى أ شبكة المقسم الحالية.
قسم الجهد
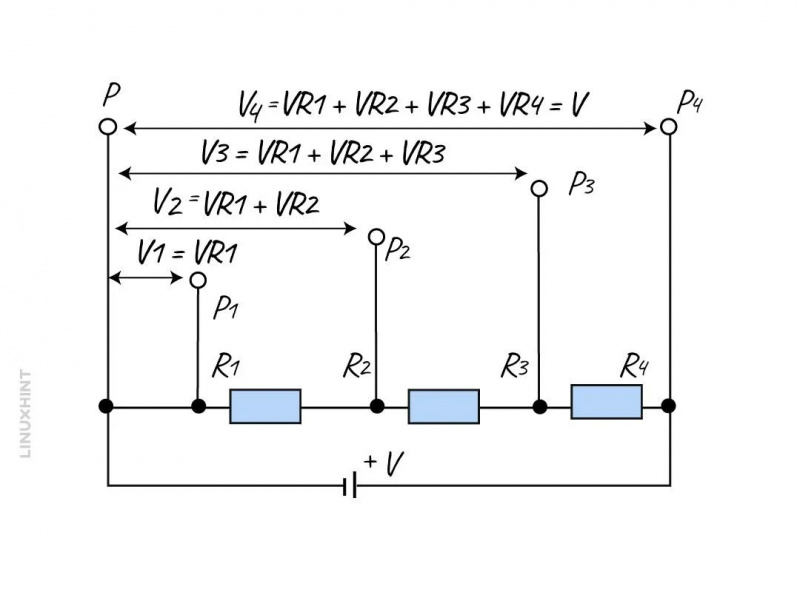
تشرح الدائرة المعطاة المفهوم الأساسي لدائرة مقسم الجهد. في هذه الدائرة، يتم توصيل مقاومات مختلفة على التوالي. هناك 4 مقاومات على التوالي اسمها ر 1 ، ر 2 ، ر 3 , و ر 4 . كل هذه المقاومات تشترك في نقطة مرجعية مشتركة وهي صفر فولت أو أرضي.
عند توصيل المقاومات على التوالي، فإن الجهد الكهربائي (في س ) يتم توزيعها عبر كل المقاوم. سترى أن كل مقاوم سوف يسقط بعض الفولتية. وهذا يعني أن كل مقاومة تحصل على حصة من الجهد الإجمالي.
بعد ذلك، استخدم قانون أوم للتعبير عن هذه الدائرة. وفقًا لتعريف قانون أوم، فإن التيار (I) الذي يتدفق عبر سلسلة من المقاومات يساوي جهد المصدر (في س ) مقسوما على المقاومة الكلية (ر ت ).
يتم إعطاء التعبير الرياضي لقانون أوم على النحو التالي
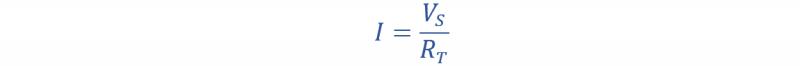
الآن استخدم قانون أوم وقم ببساطة بضرب التيار (أنا) مع المقاومة (ص) قيمة كل مقاومة
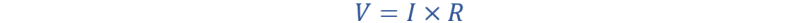
أين في يمثل انخفاض الجهد.
بعد الانتقال من نقطة إلى أخرى على طول سلسلة المقاومات، يزداد الجهد عند كل نقطة كلما قمت بجمع انخفاض الجهد. جميع مجاميع انخفاض الجهد الفردي تساوي جهد دخل الدائرة (في س ) .
ليس من الضروري العثور على إجمالي تيار الدائرة من أجل العثور على الجهد عند نقطة معينة. يمكنك استخدام صيغة بسيطة لحساب انخفاض الجهد عند أي نقطة من خلال النظر في مقاومة المقاوم والتيار المتدفق من خلاله. وهذا يبسط تحليل الدائرة ويساعد في فهم كيفية توزيع الجهد داخل الدائرة.
صيغة مقسم الجهد
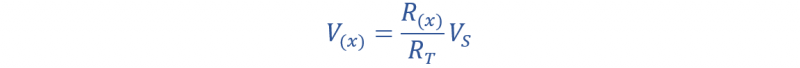
في الصيغة أعلاه، الخامس (خ) يمثل الجهد، و ص(خ) تساوي المقاومة الناتجة عن هذا الجهد. يشير الرمز RT إلى المقاومة التسلسلية الإجمالية للمقاومات وVS هو جهد الإمداد.
صيغة مقسم الجهد
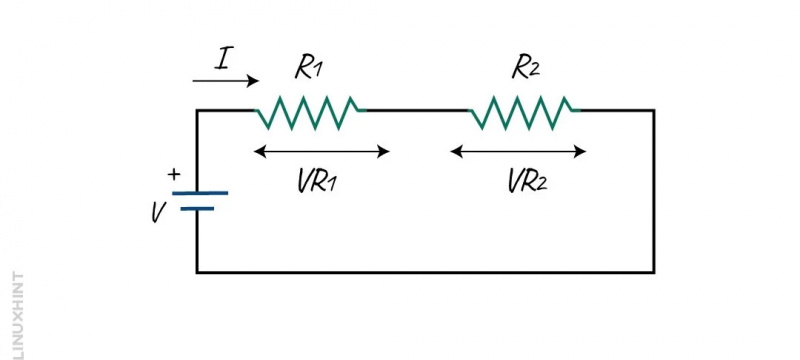
خذ بعين الاعتبار الدائرة أدناه للعثور على جهد الخرج للدائرة عبر R2 باستخدام قاعدة مقسم الجهد.
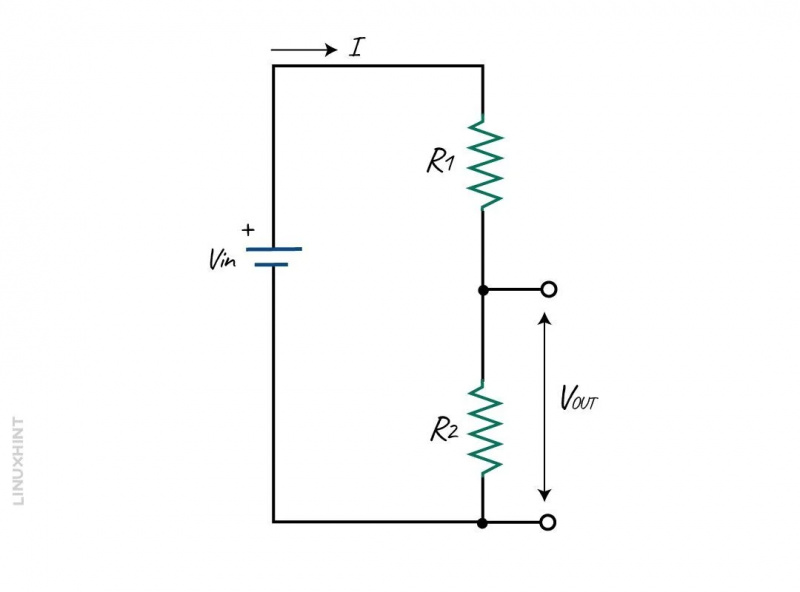
في هذه الدائرة V في يدل على الجهد العرض. إنه التيار الذي يتدفق عبر الدائرة. ويتدفق هذا التيار في كلا الاتجاهين.
دعونا نفكر في ر1 و في R2 ليكون انخفاض الجهد ر 1 و ر 2 . نظرًا لتوصيل المقاومات المعطاة على التوالي، فإن جهد الدخل V في الدائرة ستكون مساوية لمجموع كل الجهد الفردي الذي يتم إسقاطه مقابل كل مقاوم.

لحساب انخفاض الجهد الفردي عبر كل مقاومة، استخدم معادلة قانون أوم:
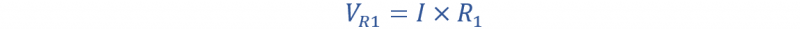
وبالمثل بالنسبة للمقاومة ر 2
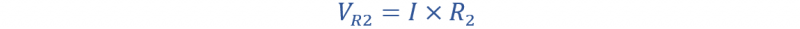
من الصورة يمكننا أن نرى أن الجهد عبر R 2 هو الخامس خارج . يمكن إعطاء جهد الخرج هذا على النحو التالي:
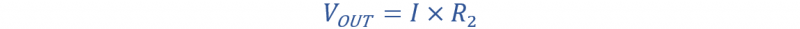
من المعادلة أعلاه يمكننا حساب جهد الدخل V في .

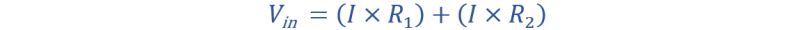
لحساب التيار الإجمالي من حيث V خارج الجهد، استخدم V أعلاه خارج معادلة.
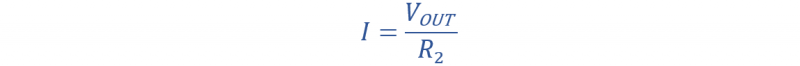
لذا فإن V خارج ستصبح المعادلة:
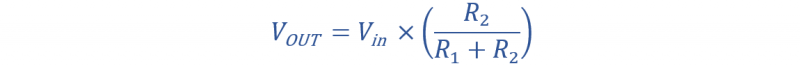
الآن فكر في دائرة مقسم جهد متعددة تحتوي على مخرجات متعددة عبر المقاومات.
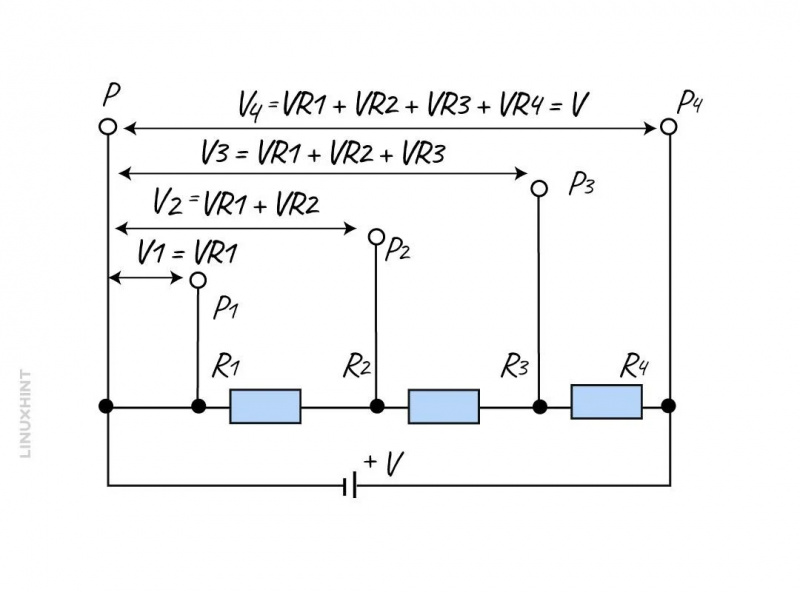
ستصبح معادلة الإخراج:
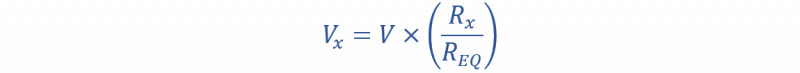
وهنا في المعادلة أعلاه في X هو الجهد الناتج.
ر X هو مجموع جميع المقاومات المتصلة في الدائرة.
القيم المحتملة ل ر X نكون:
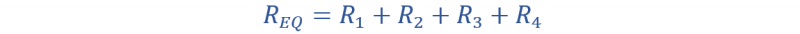
لو في لتقف على الجهد العرض. ثم يتم إعطاء الفولتية الناتجة المحتملة على النحو التالي:
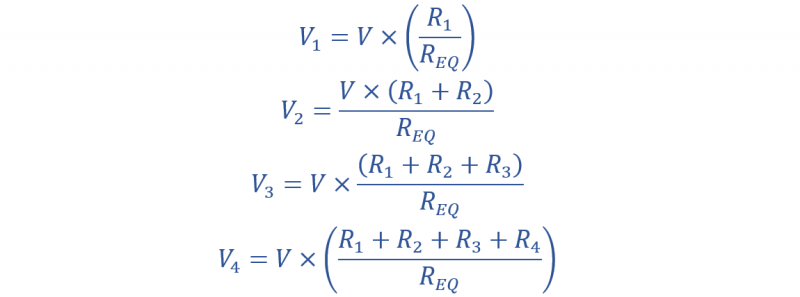
من المعادلات المذكورة أعلاه، يمكننا أن نستنتج أن الجهد المنخفض عبر المقاومات المتصلة على التوالي يتناسب مع قيمة أو مقدار المقاومة. وفقا لقانون كيرشوف للجهد، فإن الجهد المنخفض عبر جميع المقاومات المعطاة يجب أن يكون مساوياً لجهد دخل المصدر.
حتى تتمكن من العثور على انخفاض الجهد للمقاومات باستخدام صيغة مقسم الجهد.
مثال مقسم الجهد
خذ بعين الاعتبار دائرة مقسم الجهد مع ثلاث مقاومات على التسلسل، مما ينتج عنه جهدين للخرج من a 240 فولت إمداد. قيم المقاومة هي كما يلي:
- R1 = 10 أوم
- R2 = 20 أوم
- R3 = 30 أوم
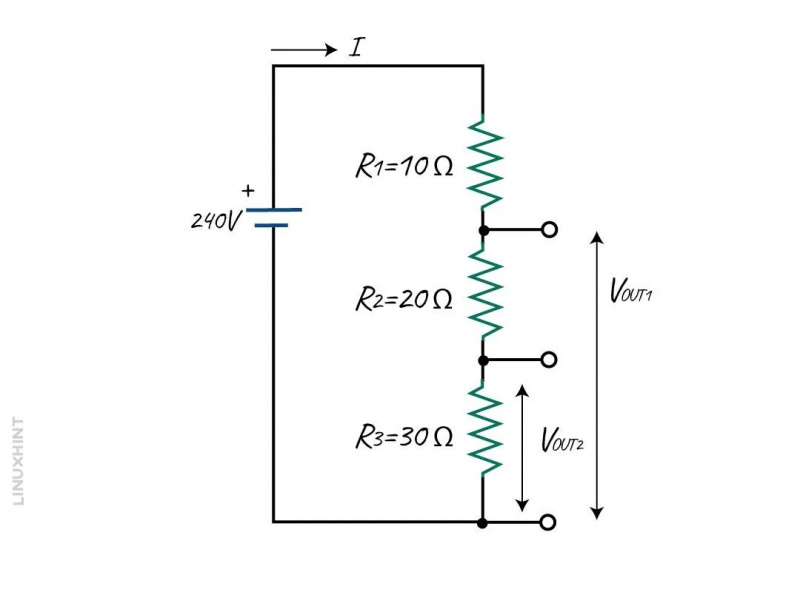
يتم حساب المقاومة المكافئة للدائرة على النحو التالي:
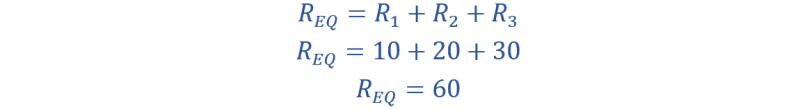
الآن يتم تحديد جهدي الخرج على النحو التالي:
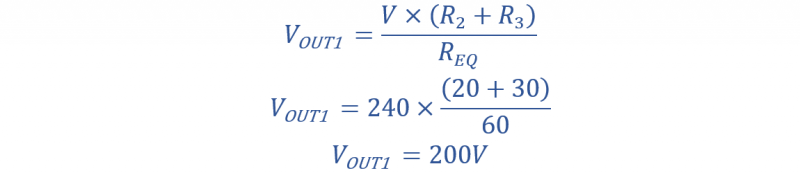
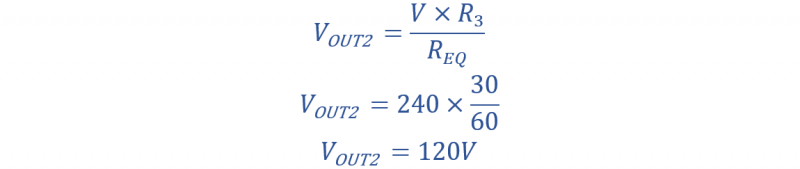
يتم إعطاء التيار في الدائرة بواسطة:
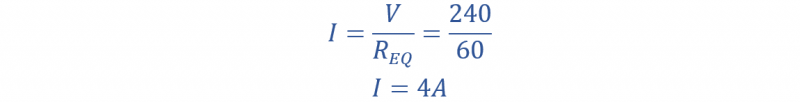
وبالتالي فإن انخفاض الجهد عبر كل مقاومة يكون كما يلي:
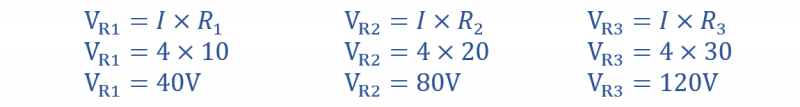
خاتمة
مقسم الجهد هو دائرة سلبية أساسية تستخدم في الإلكترونيات. يمكن لهذه الدائرة تقليل جهد الخرج بالنسبة لجهد الإدخال. يمكنك تحقيق هذا التخفيض في الجهد بعد توصيل مقاومات متعددة على التوالي. تعتمد قيمة المقاومة على قيمة انخفاض الجهد الذي تريد تحقيقه. ستقوم هذه المقاومات بإنشاء جزء جهد ثابت تحدده نسب المقاومات.
تعتبر المقاومات عناصر مهمة في الدائرة، حيث يمكنها تحديد جهد الدائرة وفقًا لقانون أوم. المقاومات الموصلة على التوالي لها تيار مستمر يمر عبر كل مقاومة. يمكنك حساب الجهد الثابت والحفاظ عليه أثناء تصميم الدوائر الإلكترونية بمساعدة صيغة مقسم الجهد.