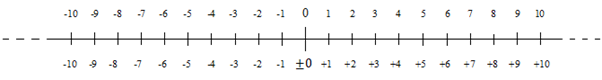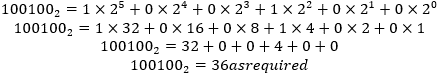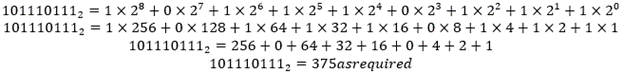المشاكل وحلولها
1. ارسم خط أعداد يحتوي على أعداد صحيحة من -10 إلى +10.
حل:
2. أضف الأرقام الثنائية التالية في تكملة 8 بت اثنين: 1010102 و11112.
حل:
3. استخدم فقط النهج المكمل للاثنين في 8 بتات لطرح الرقم الثنائي 11112 من الرقم الثنائي 1010102.
حل:
101010 في تكملة 8 بت هو 00101010.
1111 في 8 بت هو 00001111.
عكس كل 00001111 في 8 بت يعطي 11110000.
إضافة 1 إلى 11110000 يعطي 11110001.
الطرح في مكمل الاثنين هو جمع الأعداد الموجبة والسالبة المكملة للاثنين على النحو التالي:
يتم التخلص من الحمل الأخير للرقم 1 في عملية الطرح التكميلية للاثنين.
5. قسّم 36,37510 على 100010 نظامًا عشريًا وثنائيًا وقارن النتائج.
حل:
يتم استخدام استعادة التقسيم.
القسمة العشرية على أربع:
الجواب هو 36 10 الباقي 375 10 .
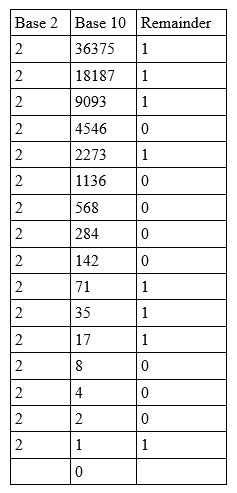
36,375 10 يجب تحويل العدد الصحيح إلى الأساس 2 كما يلي:
قراءة الباقي من الأسفل: 36,375 10 = 1000111000010111 2 .
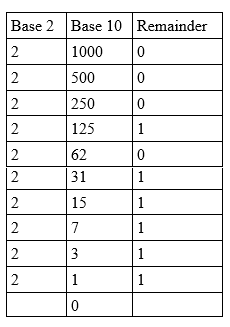
ال 1000 10 يجب تحويل العدد الصحيح إلى الأساس 2 كما يلي:
قراءة الباقي من الأسفل: 1000 10 = 1111101000 2 .
التالي، 1011000100110111 2 يقسم 1111101000 2 بالقسمة المطولة (استعادة القسمة) منذ 36,375 10 = 1011000100110111 2 و 1000 10 = 1111101000 2 (التقسيم الثنائي في عشر بتات):
يبدأ القسم فعليًا عند الجزء الحادي عشر من المقسوم نظرًا لأن البتات العشرة الأولى من المقسوم أقل من المقسوم عليه. الجواب هو 100100 2 الباقي 101110111 2 .
ولمقارنة النتائج، يجب أن يتبين الآن أن الأعداد الصحيحة للنواتج متساوية والباقيات متساوية. وهذا يعني أنه ينبغي بيان ذلك 36 10 = 100100 2 و 375 10 = 101110111 2 .
6. استخدم 8 بتات من اختيارك لتوضيح AND المنطقية، وOR، وXOR، وInvert، وShift Right، وShift Left، وRotate Right، وRotate Left. يجب أن تحتوي كل بايت على خليط من 1 و0.
حل:
- أ) اكتب الرمز الرقمي لحرف ASCII وهو الصفر بالنظام الست عشري والثنائي والعشري.
ب) اكتب الرمز الرقمي لحرف ASCII '1' بالنظام الست عشري والثنائي والعشري.
ج) اكتب الرمز الرقمي لحرف ASCII للحرف 'A' بالنظام الست عشري والثنائي والعشري.
د) اكتب الرمز الرقمي لحرف ASCII الخاص بـ 'a' بالنظام الست عشري والثنائي والعشري.
حل:
أ) '0': 30، 00110000، 48
ب) '1': 31، 00110001، 49
ج) 'أ': 41، 001000001، 65
د) 'أ': 61، 001100001، 97
8. قم بتحويل 49.4910 إلى الأساس الثاني. قم بتحويل النتيجة إلى تنسيق النقطة العائمة IEEE 32 بت.
حل:
يتم تحويل النموذج 49.4910 و49 و.49 بشكل مختلف إلى الأساس 2.
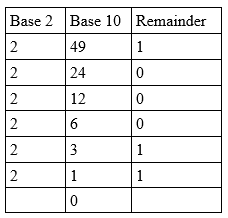
تحويل 49:
∴ 4910 = 1100012 مقروءة من أسفل العمود الأخير.
تحويل .49:
.49 × 2 = 0.98 البتة الأولى هي 0
.98 × 2 = 1.96 بتة ثانية تساوي 1
.96 × 2 = 1.92 البتة الثالثة هي 1
∴ .49 10 = 110 2 القراءة من أعلى العمود الأخير.
يعني 49.49 10 = 110001.110 2
110001.110 2 = 1.10001110 × 2 +5 في الشكل القياسي للقاعدة الثانية
'1.' بالدلالة 1.10001110 ولم يتم الإشارة إليها في النتيجة، لكن من المفترض وجودها هناك.
بالنسبة للأس، 127 10 يمثل الصفر. وهذا يعني أن مؤشر (القوة) 5 10 من 2 5 يضاف إلى 127 10 . إنه:
127 10 + 5 10 = 132 10
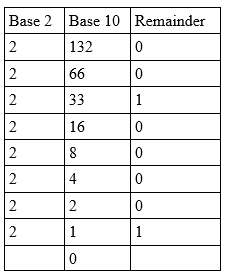
132 10 يجب تحويله إلى القاعدة الثانية ومن ثم تركيبه في حقل الأس.
إذن، 132 10 = 10000100 2
10000100 2 لديه 7 بت. الأس هو ثمانية بت. 10000100 2 لديه ثمانية بت وهذا ما يرام.
49.49 10 موجبة، وبالتالي فإن بت الإشارة هو 0. وبتنسيق النقطة العائمة 32 بت، 49.49 10 = 110001.110 2 يكون:
0 10000100 10001110000000000000000
- أ) كيف يختلف تنسيق النقطة العائمة IEEE 64 بت عن تنسيق 32 بت؟
ب) أعط السببين المرتبطين بوصف تنسيق 64 بت بأنه دقة مضاعفة أو أعلى من تنسيق 32 بت.
حل:
- - هناك 64 بت لتمثيل رقم، وليس 32.
– بعد بت الإشارة يوجد 11 بت للرقم الأسي.
– الرقم الأسي لمؤشر الصفر (2 0 ) هو 1023 10 = 01111111111 2 .
- البتات الإحدى عشرة متبوعة بـ 52 بتة للدلالة الصريحة.
- يحتوي على نطاق أوسع من الأرقام مقارنة بتنسيق 32 بت. - الأسباب التي تجعل تنسيق 64 بت يوصف بأنه دقة مزدوجة أو أعلى مقارنة بتنسيق 32 بت هو أن الفاصل الزمني بين كسرين مختلطين متتاليين، يحدهما عددان صحيحان متتاليان لتنسيق 64 بت، أصغر من التنسيق المقابل الفاصل الزمني للتنسيق 32 بت. بالإضافة إلى ذلك، هناك عدد أكبر من الكسور المختلطة المحتملة بين عددين صحيحين محددين لتنسيق 64 بت مقارنة بالتنسيق 32 بت.